2023-09-23

算法学习

secondrocker

算法

387 CHANGE ME READ TIME 1 Minute, 45 Seconds

2023-09-24 01:41

动态规划算法(DP)

动态规划算法（Dynamic Programming-DP）是通过拆分问题，定义问题状态和状态之间的关系，将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策选取那些有可能达到最优的局部解。依次解决各子问题，最后一个子问题就是初始问题的解。 https://github.com/labuladong/fucking-algorithm/tree/master/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%B3%BB%E5%88%97

47. Permutations II

# @param {Integer[]} nums
# @return {Integer[][]}
def permute_unique(nums)
  nums = nums.sort
  res = []
  used = Array.new(nums.size){ false }
  path = []
  dps(nums, path,used, res )
  res
end

def dps(nums, path, used, res)
  nums.each_with_index do |n,i|
      if path.size == nums.size
          res.push(path.dup) #unless res.include?(path)
          return
      end
      # used[i]  同层剪枝
      # !used[i-1] 标明 上一个 已完成全遍历(pop出来) /就没有遍历 [1,1,1,3] 的情况
      if used[i] || ( i > 0 && nums[i-1] == nums[i] && !used[i-1])
        next
      end
      used[i] = true
      path.push(n)
      dps(nums, path, used, res)
      used[i] = false
      path.pop
  end
end

KNN算法

K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。 归一化坐标值并计算距离： image.png 参考：https://zhuanlan.zhihu.com/p/22874873 https://blog.csdn.net/weixin_39910711/article/details/114440816

图遍历算法

深度优先

以二叉树为例，使用递归，中序遍历

def travel(node, list)
    travel(node.left, list) if node.left
    list << node.value
    travel(node.right, list) if node.right
end
先序后序只是 访问 节点顺序 不同

广度优先

逐层级，由左到右遍历

def travel(root)
   queue = [root]
   while node = queue.shift
       print(node.value)
       queue.push(node.left) if node.left
       queue.push(node.right) if node.right 
  end
end

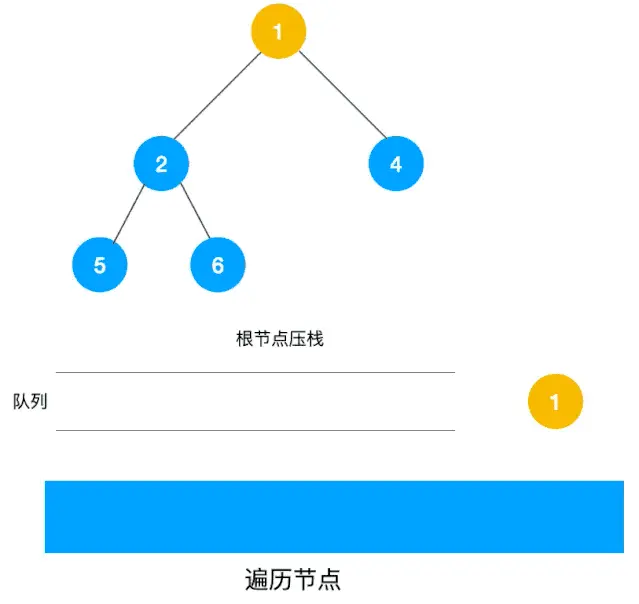image.png 会按照 1 -> 2 -> 4 -> 5 -> 6 入队列，出队列

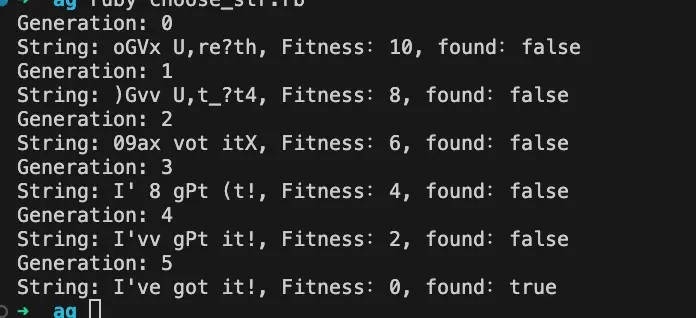
遗传算法

遗传算法模拟了自然选择的过程。那些适应环境的个体能够存活下来并且繁殖后代。那些不适应环境的个体将被淘汰。换言之，如果我们对每个个体都有一个适应度评分（用来评价其是否适应环境），那么对于适应度高的物体来说，将具有更高的繁殖和生存的机会。

另外，为了保持种族的稳定性，我们会将父代的基因传递下去

遗传算法基于一些不证自明的理论依据：

  • 种群中的个体争夺资源和交配。
  • 那些成功的（最适合的）个体交配以创造比其他人更多的后代。
  • 来自 “最适” 父母的基因在整个世代中传播，即有时父母创造的后代比父母任何一方都好。
  • 因此，每一代人都更适合他们的环境。

拿古代人类来举例子：

  • 个体（Individual）：每个生物。即每个古人类个体。
  • 种群（population）：一个系统里所有个体的总称。比如一个部落。
  • 种群个体数（POPULATION）：一个系统里个体的数量。比如一个部落里的人数。
  • 染色体（chromosom）：每个个体均携带，用来承载基因。比如一条人类染色体。
  • 基因（Gene）：用来控制生物的性状（表现）。
  • 适应度（fitness）：对某个生物是否适应环境的定量评分。比如对某个古人类是否强壮进行 [1,100]的评分。 迭代次数（TIMES）：该生物种群繁衍的次数。比如古人类繁殖了 100万年。 示例代码
# 目标
TARGET = "I've got it!" 
#基因库
GENE_BASE= "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ 1234567890, .-;:_!\c"#%&/()=?@${[]}'"
# 目标长度
LEN = TARGET.size 
# 基因库长度
GENE_LEN = GENE_BASE.size
# 族群规模
POPULATION = 1000

# 基因突变点
def mutate
  return GENE_BASE[rand(GENE_LEN)]
end

class Individual
  attr_accessor :chromosome

  def initialize(chromosome = nil)
    # 制定染色体 或 产生新染色体
    self.chromosome = chromosome || LEN.times.map{mutate}.join
  end

  #交叉算子
  def mate(par)
    new_dna = "" # 子代染色体
    self.chromosome.chars.each_with_index do |c, i|
      if rand(2) == 1
        new_dna += self.chromosome[i]
      else
        new_dna += par.chromosome[i]
      end
    end
    child = Individual.new(new_dna)
    child.mutation if rand(100) <= 20 # 概率基因突变
    child
  end

  # 基因突变
  def mutation
    t = rand(2)
    (t+1).times do
      pos = rand(LEN-1)
      self.chromosome[pos] = mutate
    end
  end

  # 适应度
  def fitness
    return @fitness if @fitness

    @fitness = 0
    self.chromosome.chars.each_with_index do |c, i|
      @fitness += 1 if TARGET[i] != c
    end

    @fitness
  end
end


cnt = 0
population = Array.new(POPULATION) { Individual.new }
loop do
  # 按适应度排序
  population.sort_by!(&:fitness)
  found = population[0].fitness == 0 # 是否找到

  puts("Generation: #{cnt}")
  puts("String: #{population[0].chromosome}, Fitness：#{population[0].fitness}, found：#{found}")

  break if found 

  new_population = []

  save_count = 10 * POPULATION / 100 # 保留精英种子(10%100)
  i = 0
  population = Array.new(POPULATION) do
    # 保留上一代的
    if i < save_count
      child  = population[i]
    else
      # 前50个有交配资格
      p1 = population[rand(50)]
      p2 = population[rand(50)]
      # 孩子
      child = p1.mate(p2)
    end
    i += 1
    child
  end
  cnt += 1
end

image.png

KMP算法